A note about sigmas

We are regularly asked about the “sigma” levels in the 2D histograms. These are not the 68%, etc. values that we’re used to for 1D distributions. In two dimensions, a Gaussian density is given by:

pdf(r) = exp(-(r/s)^2/2) / (2*pi*s^2)

The integral under this density (using polar coordinates and implicitly integrating out the angle) is:

cdf(x) = Integral(r * exp(-(r/s)^2/2) / s^2, {r, 0, x})
       = 1 - exp(-(x/s)^2/2)

This means that within “1-sigma”, the Gaussian contains 1-exp(-0.5) ~ 0.393 or 39.3% of the volume. Therefore the relevant 1-sigma levels for a 2D histogram of samples is 39% not 68%. If you must use 68% of the mass, use the levels keyword argument when you call corner.corner.

We can visualize the difference between sigma definitions:

import corner
import numpy as np

# Generate some fake data from a Gaussian
np.random.seed(42)
x = np.random.randn(50000, 2)

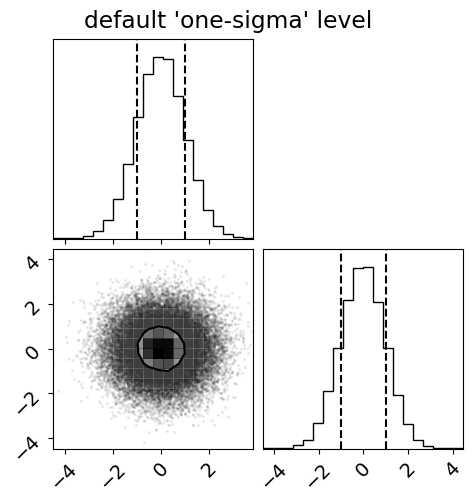
First, plot this using the correct (default) 1-sigma level:

fig = corner.corner(x, quantiles=(0.16, 0.84), levels=(1 - np.exp(-0.5),))
_ = fig.suptitle("default 'one-sigma' level")

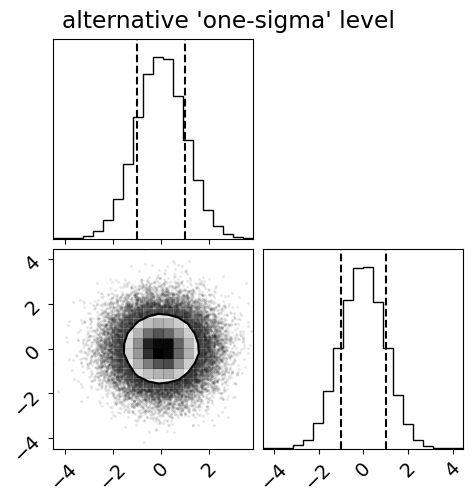
Compare this to the 68% mass level and specifically compare to how the contour compares to the marginalized 68% quantile:

fig = corner.corner(x, quantiles=(0.16, 0.84), levels=(0.68,))
_ = fig.suptitle("alternative 'one-sigma' level")